A factor is a mathematical expression composed of company-specific financial data. Factors are considered to be important in both academia and industry since some factors are correlated with the cross-sectional stock return of the companies in the future. However, such factors, often called Alpha factors, are difficult to find. In Akros Technologies, we search for alphas using AI and boost search efficiency with reinforcement learning.

To train AI models to generate factors, these factors are encoded into numerical forms. More precisely, factor expressions are converted into tensors so that the loss gradient is back-propagated. In this post, we explain how we encode factors with neural networks.

TL;DR

• We developed bi-directional factor representations: AlphaTree & AlphaStack
• AlphaTree is encoded with a node-convolutional network.
• AlphaStack is encoded with transformer encoder stack.

Bi-directional Factor Representation

A factor is a mathematical expression of financial data. Many factors are related to market anomalies. In this post, we use gross-profitability premium, the so-called GP/A factor as the main example.

Gross profit(GP) is a profit of a company after deducting the costs of goods sold from its total revenue. GP/A is a factor defined as the ratio of gross profit to the company’s assets. Since companies with higher GP/A value are considered to be more profitable, they are expected to yield higher stock returns in the future.

In its mathematical form, the GP/A factor can be expressed as follows:

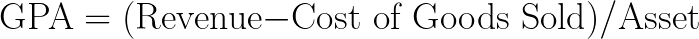
The above expression itself, however, is not an appropriate representation to implement in AI and requires a conversion to a representation comprehensible by the models.

AlphaTree

AlphaTree is a binary tree representation of a factor. The binary tree is one of the most well-known data structures in computer science. The binary tree is made of nodes that have at most two child nodes. The building block of the binary tree is the (Parent, Left child, Right child) tuple.

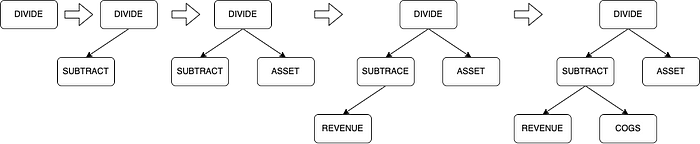
The AlphaTree representation of the GP/A factor can be visualized as follows,

The above GP/A tree has 6 nodes. DIVIDE and SUBTRACT are operator nodes that correspond to mathematical operators. Others such as ASSET, REVENUE, and COGS(Cost Of Goods Sold) are operand nodes that correspond to financial data. In actual production, we use more than two types of nodes — but for the sake of simplicity, let us just consider the operand and operator types.

Although visualization in the form of a tree is straightforward to understand, in practice, it is better to represent it as a list. The formal AlphaTree representation is given by the list of the nodes whose index is the breadth-first (level order) traversal of the tree.

The inference procedure of the AlphaTree is the same as the order of the index of the AlphaTree. The RL agent composes the tree from top to bottom, and the operand nodes are selected at the end of the inference. In this sense, AlphaTree is considered to be a top-down representation.

AlphaTree is a top-down representation of a factor

AlphaStack

AlphaStack is a stack-based representation of a factor. It is easier to explain the AlphaStack with a concrete example directly, so let us show the AlphaStack representation of the GP/A factor.

At the first glance, the AlphaStack representation seems to be not much different from the AlphaTree except for the indexing order. However, the evaluation process of AlphaStack does in fact make significant differences.

The AlphaStack uses a stack data structure to evaluate the factor. Let us first consider an empty stack. Then, we essentially keep popping out the first element of the list and putting it in a stack. If the popped element is an operator node, we pop operands in the stack, put them as arguments of the operator, and then put the evaluated data into the stack. This procedure is repeated until all element in the AlphaStack list is popped. The following figure explains the evaluation procedure for the GP/A factor.

The inference procedure of the AlphaStack is the same as the order of the index of the AlphaStack. The RL agent creates the list from left to right with a condition that the operand nodes are selected first. Since operands are located at the bottom of the factor tree, AlphaStack is considered a bottom-up representation.

AlphaStack is a bottom-up representation of a factor

A single factor can be represented in terms of both AlphaTree and AlphaStack. By exploiting the complementary properties of those two, the agent learns to search for alphas in the factor space more efficiently.

Factor Encoder

Once we set up the systematic representations of factors, we encode them to numerical tensors.

Encoding AlphaTree

The first step of factor encoding is to assign integers to each node which is analogous to the tokenization in NLP. We call the tokenization dictionary a Codebook. The codebook should remain unchanged for re-training and transfer learning of RL models, and so we manage our codebook history in our database.

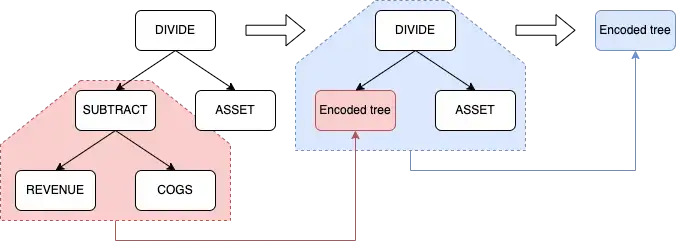
After passing through the codebook tokenizer, the factor turns into the inter-component tensor. The tokenized tensor passes the embedding layer that transforms an integer into a float-component tensor with a fixed dimension.

The next step is to combine those lists of tensors into a single tensor. The simplest way is to concatenate them, but such a way does not properly reflect the original tree structure or compress the tensors effectively.

We are encoding AlphaTree by exploiting inductive bias inspired by the one used in the convolutional neural network (CNN). In CNN, the nearby pixels are aggregated to a combined pixel. In AlphaTree, the nearby nodes are aggregated to a combined sub-tree. The following figure depicts how AlphaTree is encoded with node convolutions.

In conclusion, the full encoding network of AlphaTree has the following architecture.

AlphaTree is encoded with a node-convolutional network

Encoding AlphaStack

The first few steps of the AlphaStack encoder are the same as the AlphaTree until the embedding layer. To further encode AlphaStack in a representation-specific way, we use the self-attention mechanism of the transformer encoder stack. More specifically, the HuggingFace BertModel.

The input structure of BERT is given by the classification(CLS)-token followed by the tokenized words in a sentence or two. The CLS token is a special symbol used as the output of various sentence-wise tasks such as sentence classification. Therefore, the CLS token can be used to summarize the sequential information of the whole sentence into a single token.

In HuggingFace BertModel, the output of the CLS token is provided as the pooler_output. The simple code snippet below shows how to use HuggingFace BertModel in Jupyter Notebook.

The key idea of the AlphaStack encoder is to view a factor as a sentence and use pre-developed network architecture in the NLP domain. To summarize, the full encoding process of AlphaTree has the following architecture.

AlphaStack is encoded with transformer encoder stack

The complementary properties of AlphaTree and AlphaStack also exist in their encoders. AlphaTree encoder uses CNN-like layer first developed in Vision-domain while AlphaStack encoder uses transformer first developed in NLP-domain. Due to their opposite properties, the AlphaTree-based agent tends to focus on how to normalize or preprocess the operands, while the AlphaStack-based agent tends to focus on the operand selection and combination.

Conclusions

• We developed two complementary factor representations: AlphaTree (Top-down) & AlphaStack (Bottom-up)
• AlphaTree is encoded with a node-convolutional network
• AlphaStack is encoded with a transformer encoder stack.

I would like to emphasize that factor encoding is merely a starting point of the RL-based factor search. The important part is to properly incorporate the encoder network into the RL agent. What we are doing after encoding the factors will be discussed in the upcoming posts. Stay tuned!