The series on the topic of Exploration in Reinforcement Learning consists of the following 4 sections.

Part 1: Background & Traditional Approaches
Part 2: Modern Strategies for Exploration
Part 3: Implementation & Simulation
Part 4: Application of Exploration Problems relevant to Akros Technologies

Introduction

The trade-off between exploitation and exploration is a well-known problem in reinforcement learning that has come to light by the Multi-armed bandits.

Background: Multi-Armed Bandits

The problem considers a scenario where an agent has multiple decisions to make:

(i) an agent has the choice as to which bandit to play with
(ii) an agent has the choice to play as many times as the agent wants to play on the current bandit given the experience with it thus far or to switch to a different bandit

In other words, the agent can either exploit the current information it has and decide to go for the bandit that gives the highest expected reward given the previous experience and past observations, or explore other options and opt to try a different bandit that may turn out to yield higher reward.

Background: offline vs. online

The notion of offline and online comes into play to refer to how an agent is trained. Offline training is where an agent learns from the static dataset consisting of historical observations. Online training is where an agent learns from a live dynamic stream of data. In the real world, online training is therefore more difficult as the agent has to take the next action within a time constraint. As difficult as online training can get, the agent learns to adapt to the dynamics of the environment which is especially important in versatile environment settings.

Background: extrinsic motivation vs. intrinsic motivation

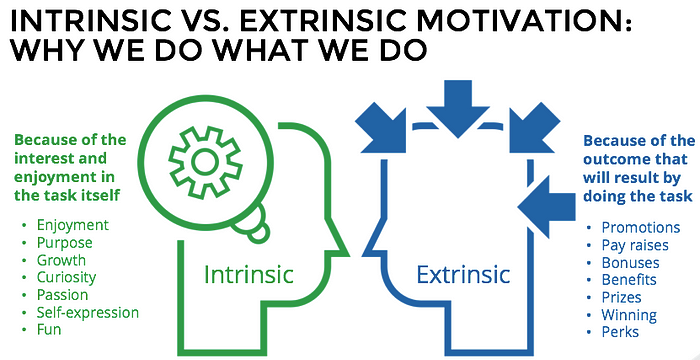
The term extrinsic motivation denotes a motivation that stems from a specific reward outcome. In games like Atari, an extrinsic reward may be quite straightforward to define in the form of a numerical score. In relatively more complex games like Chess and Go, there may be more complex goals in addition to simply defined rewards such as those coming from taking the opponents’ horses. Since the ultimate aim of the game is to win, it is a sensible idea to create a discounted reward function — a function, for instance, rollouts the game until the very end, and discounts the rewards back to the present timestep depending on the ultimate outcome of the game.

The term intrinsic motivation refers to a motivation that is driven by something other than the explicit reward. In psychology, intrinsic rewards are to stem from non-reward specific stimuli such as enjoyment, growth, and curiosity. In the context of reinforcement learning, there have been different ways of formulating and numerating intrinsic rewards —further details of which will be discussed later.

Background: deterministic vs. stochastic
The difference between deterministic and stochastic settings is usually based on the environment in which an agent is situated. Given the current state and the set of actions that have been taken to reach that state in a deterministic environment setting, the same action will always lead to the same outcome. In a stochastic environment setting, however, the same action will not always lead to the same outcome. Whereas in a game of chess it is deterministic for a horse to move from A5 to A6 for instance, in a probability game involving dice, it is not deterministic for the dice to give a specific outcome.

This article carefully analyses the traditional approaches for exploration as well as relatively modern approaches that have been taken to analyze intrinsic motivation in order to address the apparent tradeoff between exploitation and exploration. Here we go!

Traditional Methodology

Greedy Strategy
The greedy strategy is to take the optimal action that the model suggests given the historical observation and past actions experienced so far. The decision is therefore to take an optimal action that maximizes the value of the state-action pair given by:

The danger associated with the greedy strategy is that the agent may continue to take a sub-optimal action. By continuing to take the action that maximizes the expected reward, the agent may choose to play with a sub-optimal bandit, when in fact there is another bandit which gives a higher reward. A greedy strategy is therefore an exploitation strategy at its fullest with no particular room for a search for an alternative action that may give a better outcome.

ε-Greedy Strategy
Given a value of ε between 0 and 1, the epsilon greedy strategy is to generate a policy where an agent takes a random action with probability ε and takes an optimal action that is expected to maximize reward with probability 1-ε.

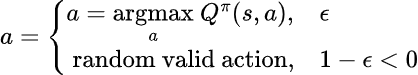
There are two problems with the epsilon greedy strategy. The first is that even if the optimal strategy has been found, the agent will with probability ε take a random action. The second problem is that the value of ε essentially becomes a hyperparameter that is usually determined empirically — using a number that simply outputs the highest rewards through experiments.

Upper Confidence Bound Strategy
A marginal improvement from the epsilon greedy strategy is the upper confidence bound (UCB) strategy, which adjusts the balance between exploration and exploitation through the interaction between the agent and the environment. A UCB strategy is an example of a count-based exploration strategy. The strategy accounts for the number of times that a particular action has been taken so far — the fewer the number of times that the action has been taken in the past, the strategy adds a greater intrinsic motivation for the agent to explore that particular choice of action. Formally:

The first term in the equation is identical to a greedy strategy — it is an aspect of the equation that encourages to take the action that is expected to give a maximum reward. The second part of the equation encourages exploration, the degree of which is adjusted according to the value of the constant c. The value inside the square root very much depends on the value of the denominator which increases at a faster rate than that of the nominator, as the latter is slowed down by the log function.

N(a) is simply a function that counts the number of times that the chosen action had been taken in the past. The incentive to explore will therefore be greater for actions that have been selected infrequently.

Thomson Sampling Strategy
The key difference between the Thomson sampling strategy and the other traditional strategies is that the former calculates the confidence level of the expected reward through Bayesian optimisation. To perform Bayesian inference, the first step is to set up a prior depending on the form of the expected outcome. To further illustrate:

Bernoulli Distribution: if the expected reward is in the form of binary output
Uniform Distribution: if the expected reward is between certain extremes
Normal Distribution: if the expected reward has a slight variation over an average value

Whether it be Bernoulli Distribution, Uniform Distribution, or Normal Distribution, the initial distribution that we assume for the output from the bandit is called the prior. It is therefore the probability distribution of the possible outcome before taking into consideration any observation from the bandits. Once we begin to obtain a specific reward, the likelihood function of each bandit can be updated to reflect the rewards that it had given. The prior and the updated likelihood function gives a posterior probability distribution from which appropriate action can be selected.

The Thomson sampling strategy takes into account the confidence level of the distribution to reflect its choice of action. Whereas the greedy strategy always opts for an action that is likely to return the highest expected reward even if the level of confidence is low, Thomson sampling strategy adjusts the selection according to the confidence level of the posterior probability distribution of the possible actions.

Concluding Remarks
We have so far discussed the background of reinforcement learning in the context of exploration and the traditional ways of motivating an agent to explore. In the next section, we will implement the effectiveness of the strategies in a simulation, and over the course learn about modern strategies.